Anna Montemurro
ABSTRACT – The present article contains a
study on triangles.
Such a study shows how to reach the solution
of a triangle using an innovative method which does not require difficult
reasonings or complicated trigonometrical formulas, but simply uses the
concept of ratio between two quantities.
1. Introduction
The work
begins with some observations on the triangles. They follow the demonstrations
of two new theorems. The demonstration of an innovative method for the solution
of the triangles and some examples of application.
2.
Observations on triangles
We want to construct one of the innumerable
triangles that has the altitude given, for example of 2 cm and to calculate the
measures of its sides. (Fig. 1).
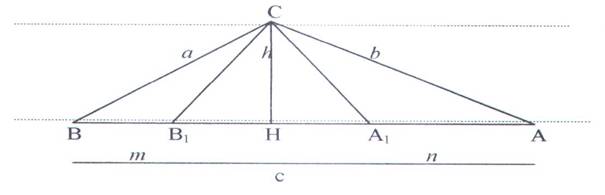
Fig. 1
We can go on as follow:
first we multiply the measure h of the altitude CH for any greater
number than the unit,, said factor k
, then for its inverse, that is for ![]() and the products so obtained are considered
respectively as the amount of the side a and
of its projection on the base that is m
and as their difference, for which it results:
and the products so obtained are considered
respectively as the amount of the side a and
of its projection on the base that is m
and as their difference, for which it results:
![]() (1)
(1)
![]() (2)
(2)
This process finds confirmation, multiplying
member to member the (1) and the (2),we obtain the known relation:
![]() (3)
(3)
Now,
knowing the amount and the difference of two segments, to find the measure of
each of them, it is sufficient to apply the following formulas:
![]() (4)
(4)
![]() (5)
(5)
Replacing
the corrrisponding values of the (1) and
(2) with the (4) and (5),we obtain:
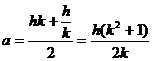 (6)
(6)
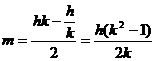 (7)
(7)
With a
method similar to the previous one, choosing another major number than the
unit, said facto ![]() ,
, ![]() and
and ![]() are built
and the measures b and n are calculated.
are built
and the measures b and n are calculated.
Therefore we have:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
The (6) and
(7), (10) and (11) allow to calculate
the measures of the sides of one of the endless triangles that have the
altitude of 2 cm, built by us. As among
the endless triangles that have the altitude of 2 cm, there are also the
right-angled triangles (in which such
altitude becomes that relative one to the hypotenuse),we ask:
what is the
relation that lies![]() and
and![]() in such triangles?
in such triangles?
That is, if
for example k = 6, what value will
take![]() so that such
triangle is rectangle?
so that such
triangle is rectangle?
From the
previous observations the theorem k (by Montemurro) and the
theorem of altitude (by Montemurro) originate.
3. Theorem k (by Montemurro). In every right-angled
triangled, if we have
![]() e
e ![]() then:
then:
![]() .
.
DEMONSTRATION. Given a right-angled triangle ABC, right Ĉ,
we draw the altitude relative to the hypotenuse and a, b,
c, m, n, h, are respectively the measures of the catheti, of the
hypotenuse, of the projections of the catheti on the hypotenuse and the
altitude relative to it(Fig. 2).
Fig.2
![]()
![]()
 C
C
a h b
m n
![]() B
H A
B
H A
c
![]()
It is
well-known that :
![]() (12)
(12)
Replacing
in this last one to a, b, c, the formulas we have found previously in the introduction,
that is:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
We have:
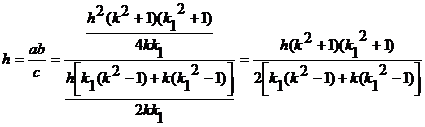 (16)
(16)
From this
last one, dividing for h ≠0
both the members of the equality, we have:
![]() (17)
(17)
The (17)
can be formulated easily in the following way:
![]() (18)
(18)
and,
resolving as to k1 , being
the discriminant of the above-said equation similar to zero, we obtain:
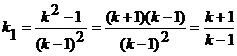 (19) c.v.d.
(19) c.v.d.
To reply to
the question given in the introduction, if ![]() = 6, then:
= 6, then:
![]()
4. Corollary 1. One of the consequences of the theorem
![]() is that,
replacing
is that,
replacing ![]() in the (10) and (11) and in all the forms in which it appears with
the value
in the (10) and (11) and in all the forms in which it appears with
the value ![]() , we
have all the elements of a right-angled triangle in function of h and
k :
, we
have all the elements of a right-angled triangle in function of h and
k :
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25) where 2p indicates the perimeter
(25) where 2p indicates the perimeter
![]() (26)
(26)
![]() (27)
where
ri is inradius
(27)
where
ri is inradius
![]() (28)
(28)
Observations.
- Relating the
previous formula two by two, we can have the other ones.
Examples.
from (20)
and (22) we have: ![]() (29)
(29)
from (24)
and (22) we have: ![]() (30)
(30)
from (20)
and (25) we have: ![]() (31)
(31)
from (25) and (26) we have: ![]() (32)
(32)
- Adding member to member the (1)
and the (7) we obtain the following notable ratio that is very useful
in the resolution of some problems.
![]() (33)
(33)
- For the similarity of the
right-angled triangles BHC, AHC, …
(Fig.2) there are the following chains of equal ratios :
![]()
![]()
- Two right-angled triangles are similar if,
and only if, they have the same value of k .
6. Theorem of altitude (by Montemurro). In every triangle if we put
![]() and
and ![]() then:
then:
![]()
Note. From now on, for facility of study, the differences ![]() e
e ![]() will be indicated respectly with the letters e and
f .
will be indicated respectly with the letters e and
f .
DEMONSTRATION. We consider any kind of triangle
ABC, with the base AB, we draw the altitude relative to it and they are h, e, f
respectively the measures of the altitude CH, of ![]() and
and ![]() (Fig.4).
(Fig.4).
|
Fig.4 |
![]()
![]()
C
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 e f
e f
![]()
![]() a h b
a h b
![]() B m H n A
B m H n A
![]() c
c
We want to
demonstrate that:
![]() (34)
(34)
The relation (34) is demonstrated easily because it is given multiplying member to member the (2) and (9)
of this work.
As the product ![]() is only a number and
is only a number and ![]() expresses
the area of the rectangle having for dimension
expresses
the area of the rectangle having for dimension ![]() and
and ![]() , the theorem of the altitude can be explained geometrically in the
following way:
, the theorem of the altitude can be explained geometrically in the
following way:
In each triangle the
square built on one of its altitudes is equal to as many rectangles congruent
among them, each one having for dimension the measures e and f , as the product kk1 indicates .
In the
right angled triangle the theorem of the altitude takes a particular importance
for the relation that is between k
and k, .
7. Corollary 2. One of the consequences of the theorem of the altitude of a triangle is
the formation of the following chain of
notable reports:
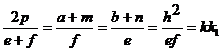 (35)
(35)
DEMONSTRATION. With reference to the picture 4, we
consider the right angled triangles BHC
and AHC.
Applying to each of them the theorem of
Pitagora, we have that:
![]() (36)
(36)
![]() (37)
(37)
Equalizing
the second members of the (36) and (37)
, we have :
![]()
That becomes :
![]()
and, for
the property of to makeup:
![]() (38)
(38)
As the
differences ![]() and
and ![]() have been called respectively e
and f
we have:
have been called respectively e
and f
we have:
![]() , from wich we obtain:
, from wich we obtain:
![]() .
(39)
.
(39)
For the
equality: ![]() , we can write:
, we can write:
![]() .
.
Putting in
the (39) ![]() , we obtain:
, we obtain:
![]() (40)
(40)
For the
theorem of the altitude ![]() the (35) is
shown.
the (35) is
shown.
Note. A reader can verify that, leaving from one of
the notable ratios of (35), we can obtain some useful formulas for the resolution
of any triangle.
For example, applying the property of the
factorizing to the proportion which is obtained from the ratio ![]() , we have:
, we have:
![]() (41)
(41)
Other
formulas, which we can obtain easily
manipulating those given before,
are :
![]() (42)
(42)
![]() (43)
(43)
.
.
8. Trigonometric nature of k
From the
relation ![]() we obtain that:
we obtain that: ![]() (44)
(44)
Putting in
the (44):
![]() we have:
we have:
![]() from which we obtain:
from which we obtain:
![]() (45)
(45)
Resolving
the system:
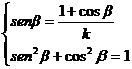
We have:
![]() (46)
(46)
![]() (47)
(47)
9. Description of the
innovative method
The innovative method for the resolution of a triangle consists in
putting always in ratio the measures given in order to calculate the value
k if we
deal with a rectangle triangle, or the values k and k1 if we deal with any kind of triangle.
Found the value
k or the values of k
and k1, we calculate the
measures required using the formulas that derive from the present work.
10.
Applications to the right-angled triangles
In the treatment of the following problems we will follow the literal
indications of the picture 5.
![]()
![]() C
C
![]()

 e f
e f
![]() h
h
![]() a b
a b
Fig.5
![]() m n
m n
B H A
c![]()
·
The perimeter and the altitude
relative to the hypotenuse of a right-angled triangle are respectively 14,4 cm and 2,88 cm. To calculate the measures of the sides of the triangle.
Putting the
measures given in ratio and utilizing the (33), we have:
![]()
From which,
resolving the equation in k , we find
that ![]()
Therefore,
we obtain the measures required:
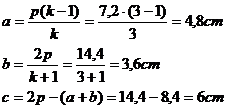
- Is it possible to build a right-angled triangle that has 2p=136 cm,
m=45 cm ?
Solving the
equation in k which is obtained from
the rapport of the measures given with the use of the (25) and (21) and leaving
the roots ![]() , we have that
, we have that ![]() . So , the
answer to the question is affermative.
. So , the
answer to the question is affermative.
To
calculate the measures of the sides of the triangle we apply the same formulas
of the previous exercise.
- In a right-angled triangle we have : a =18 cm; ri =6 cm. To calculate the
measures of the other sides of the triangle.
We put in ratio the measures given, using the
(20) and (27):
![]()
Therefore, we get ![]() and the measures required are obtained
respectively from the ratio of (22) and (20); (24) and (20) :
and the measures required are obtained
respectively from the ratio of (22) and (20); (24) and (20) :
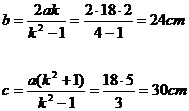
- In a right-angled
triangle we have:
a+b = 41 cm; c= 29 cm.
To calculate the measures a and b.
From the ratio :
![]()
We obtain
that k = 2,5
Known the
value k easily we calculate a = 21 cm and b = 20 cm, applying opportunely the
formulas that we find in this work.
- Two right-angled triangles are similar and have respectively:
A1 = 456,30 cm2 ( the first);
a = 31,2 cm; n =
5 cm ( the second).
To calculate the perimeter of the first triangle and the ratio of
similarity .
Note. The
ratio of similarity will be indicated with the letter R.
By the
ratio between a and n of the second triangle we find k=5.
As the two
triangles are similar, the value k of
the first of them is 5 too.
Therefore, applying
opportunely the formulas obtained from the present work, we have:
![]()
![]()
![]()
- Applications to any triangles
- A triangle of area 360 cm2 is divided by the altitude in two parts
so that:
![]()
To establish if the triangle given is a
right-angled triangle or if is not. To calculate the measures of the sides of
the triangle.
We observe
that, for the theorem k, the relation
![]() is not true
for k = 2,5; therefore we conclude
that the triangle given is not a right-angled triangle.
is not true
for k = 2,5; therefore we conclude
that the triangle given is not a right-angled triangle.
With the
inverse formula of the (42) we calculate the measure of the altitude which is
of 20 cm.
Therefore we have:
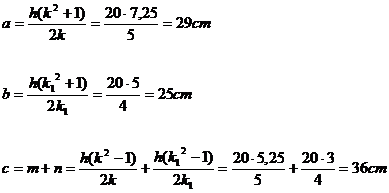
- To calculate the measures of the altitude and the sides of a
triangle, knowing that:
a+b=150; c=120cm;
k = 6
We use the following notable ratio:
![]()
If kk1
= 9 and k =
6, then k1 = 1,5
From: ![]()
We find that:
![]()
Therefore:
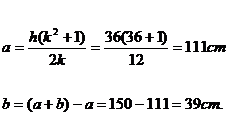
- Two similar
triangles have respectively:
2p=216cm; h=18cm;
(the first)
and,
m1=120cm, n1=36cm; (the second).
To establish the ratio
of similarity of the two triangles.
Note. The
ratio of similarity of the two
triangles will be indicated with the letter R.
From the first triangle we obtain:
![]() .
.
From:
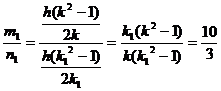 we have:
we have:
![]()
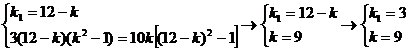
Therefore:
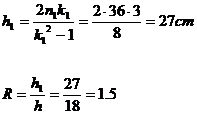
·
Two similar triangles have
respectively:
a+b=50cm; c=40cm (the first);
a1
= 92.5cm; h1 =30cm
(the second).
To
establish the ratio of similarity and to calculate the measures a, b of the first triangle.
NOTE The ratio of similarity of the two triangles will be indicated with the
letter R..
From the
first of the two triangles we obtain the
value kk1 expressed
from the ratio ![]()
From the
second triangle we calculate the value k
that is given from the ratio:
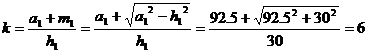
As the two
triangles are similar, they have the same values k e k1 so, replacing in kk 1= 9 the value k=6
we have that k1=1,5
![]()
So we have that:
![]()
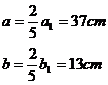
- To resolve a triangle ABC, with base AB, knowing that:
a+ c =77cm; b=13cm;
k=6
We calculate, as usual, the ratio among the
measures given ![]() , and we put in it :
, and we put in it :
![]()
![]() ;
; ![]() ,
,
that is:
![]() (we remember that k stands for 6).
(we remember that k stands for 6).
Resolving the equation which is obtained from
the previous relation and ruling out the root <1, we obtained that k1
= 1.5.
Therefore, we have:
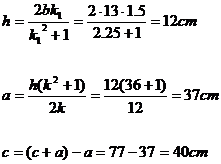
- To resolve an obtuse-angled triangle ABC, with base AB, knowing
that :
a+c=112cm; b=104cm;
k =13/6
C
![]()

h a b
![]()
![]()
![]() H m
H m
![]() B c A
B c A
![]() n
n
In this
case, as the triangle given is obtuse-angled, the foot of the altitude falls on
the prolongation of the side AB; therefore, for definition, the value k
given refers to the ratio ![]() .
.
We utilize
the data of the problem finding, as usual, the ratio among the measures known,
that is:
![]() (1).
(1).
Putting in the (1) :
![]()
and, resolving the equation that we obtain,
that is:
![]() (we remember that
(we remember that ![]() ), we
establish
), we
establish
The value k1=3
, excluding the root equal to 9 which
refers to the acute minor angle.
So we calculate the measures required:
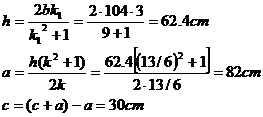
Observation.
When the size of the
obtuse angle of a triangle is given , to calculate the value k ,first it is necessary to find the
supplementary angle of that one given and, then, to apply the formula ![]() .
.
11. Conclusion
We can resolve a
triangle, that is we can calculate all its elements: sides and angles, following the tracking models reported here
on end and already indicated in the 9. point in the description of the
innovative method.
“We calculate the ratio among the measures known at the
end to find the values k and k1 and we apply
opportunately the formulas which flow from this work”.